1 各种双极性SPWM波形生成方法的开关点计算
1.1 自然采样法
当载波比为N时，在逆变器输出波形的一个周期内，正弦波与三角波有2N个交点，如图（1a）所示。根据相似三角形定理可得：
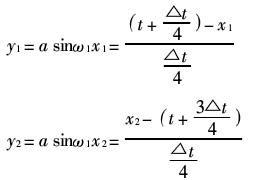
解上述方程可得：
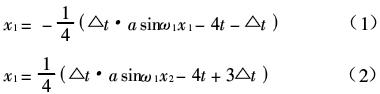
其中，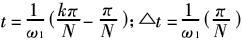
。N为载波比，即半个周期内的脉冲个数；K为第k个脉冲；a为调制度，与频率ω1有一定的函数关系。按迭代法计算，取初值为x10=x20=0，当迭代精度取xi+1-xi<10-6时停止计算。
1.2 规则采样法
在三角载波的每一周期内的固定时刻找到正弦调制波上的对应点，用此值对三角载波进行采样。根据采样时刻的不同可分为规则采样法一、规则采样法二及不规则采样法。
（1）规则采样法一
如图（1b）所示，固定在载波正峰值处（即时刻t）对正弦波采样，延长与三角波相交，从而确定开关点x1、x2的时刻。
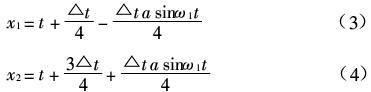
（2）规则采样法二
如图1（c）所示，固定在载波负峰值处即
时刻对正弦波采样，延长与
三角波相交，从而确定开关点x1、x2的时刻。根据相似三角形定理可得：
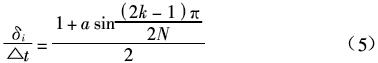
（3）不规则采样法
在三角载波每一周期内的正峰值和负峰值处找正弦调制波上的对应点，即时刻t和时刻(t+Δt/2)两处采样，如图（1d）所示，得开关点x 1、x 2的时刻为：
1.3 面积等效法
面积等效法如图1(e)所示，设脉宽为δk，脉冲间隙分别为δk1和δk2，脉冲幅值为Us/2。由第k份正弦波面积与对应的第k个双极性SPWM脉冲面积相等可求出开关的时间。根据参考文献[2]得式(11)～式(13)：
按以上计算方法，当正弦波半个周期内的采样点数N为任意整数（N为3的整数倍）时，可用计算机算出上述五种方法的开关点数据，现列出N=6时五种方法的开关点数据及总谐波失真度，如表1所示。
2 双极性SPWM脉冲序列谐波分析
双极性SPWM逆变器输出为一串周期性脉冲序列。为简化推导公式，假设该脉冲序列波形为周期性奇函数，周期为2π，将正弦波信号的正负半周分别平均分为N等份（N为3的倍数）。在(0,π)内其数学表达式为（以第k个脉冲为例，k=1,2,…,N）：
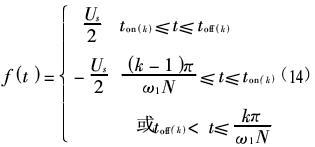
将f(t)按傅立叶级数展开可得下式：
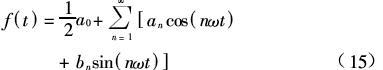
由于输出波形为奇函数，可得：
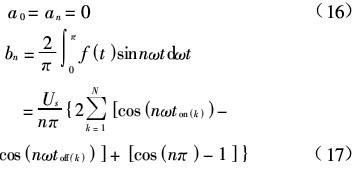
并得：
总的谐波失真度为：
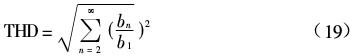
其中：n为第n次谐波，bn为第n次谐波的幅值，b1为基波的幅值。
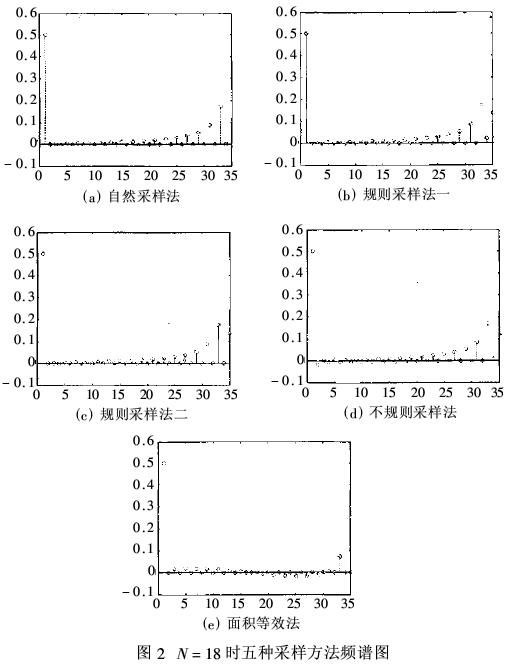
本文给出N=18、a=1时各方法的频谱图，如图2所示。
3 结论
从表1及图2可以看出，THD值越小，表明谐波失真越小，抑制谐波能力越强。从各种THD值的比较及频谱图得知，抑制谐波能力自然采样法最好，谐波的幅值明显最小，其它依次为面积等效法、不规则采样法、规则采样法二、规则采样法一。此外，从各种不同取值计算及仿真得知，以上所有方法均可抑制最低次为2N-1次以下的谐波。就同一种算法，随着N的增加，抑制能力均增加，谐波的幅值也明显减少。因此，看不出各方法有何明显区别，但由于自然采样法需解一个超越方程，难于求解，而对于不规则采法，在一个载波周期里采两次正弦波值，比规则采样法二和法一的采样次数增大一倍，这增大了数据的存储量。因此，一般采用较准确的规则采样法二及面积等效法。
参考文献：
[1]陈伯时.电力拖动自动控制系统[M].北京：机械工业出版社，1992.
[2]廖晓钟，金英.一种改进的生成SPWM波形的等面积算法[J].北京理工大学学报，2（16）：710-714.
[3]李宏，焦振宏，周继华，李治典.SPWM波形等面积动态递推算法[J].西北工业大学学报，18(2)264-266.
[4]钟福金，钱昱明，王晓军.交流变频调速系统的SPWM波形生成方法的谐波分析[J].南京航空航天大学学报，（增刊）94-98.
[5]陈国呈.PWM变频调速技术[M].北京：机械工业出版社，1998.
